Introducción al análisis de datos con R

Una introducción al lenguaje de programación

Xavier Clemente García

Objetivo

Aprender como describir datos, formular hipótesis, validar supuestos y aplicar pruebas estadísticas en R.

Estadística descriptiva

Medidas de tendencia central Existen varias pruebas que nos permiten describir la composición y comportamiento de nuestros datos.
Vamos a clasificar medidas de tendencia central y medidas de dispersión

Estadísticos	Definición
Media	Se refiere al promedio de un conjunto de datos
Mediana	El valor que se encuentra en la mitad de un conjunto de daots

Medidas de dispersión

Estadísticos	Definición
Desviación estándar	Qué tan dispersos están los datos en un conjunto
Varianza	Dispersión de los datos entorno a la media
Rango	Diferencias entre valores máximos y mínimos en una muestra de datos

Ahora trabajaremos con dos bases de datos PlantGrowth y Palmerpenguis

Primeros pasos con PlantGrowth

Medidas de tendencia central

data("PlantGrowth")
mean(PlantGrowth$weight)

[1] 5.073

median(PlantGrowth$weight)

[1] 5.155

Medidas de dispersión

sd(PlantGrowth$weight)

[1] 0.7011918

var(PlantGrowth$weight)

[1] 0.49167

range(PlantGrowth$weight)

[1] 3.59 6.31

Otra función

summary(PlantGrowth$weight)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  3.590   4.550   5.155   5.073   5.530   6.310 

Distribución de los datos

Antes de partir en un análisis de normalidad puede ser interesante oberservar como se distribuyen los datos.
Para entender esto, habrá que partir desde un ejemplo básico.

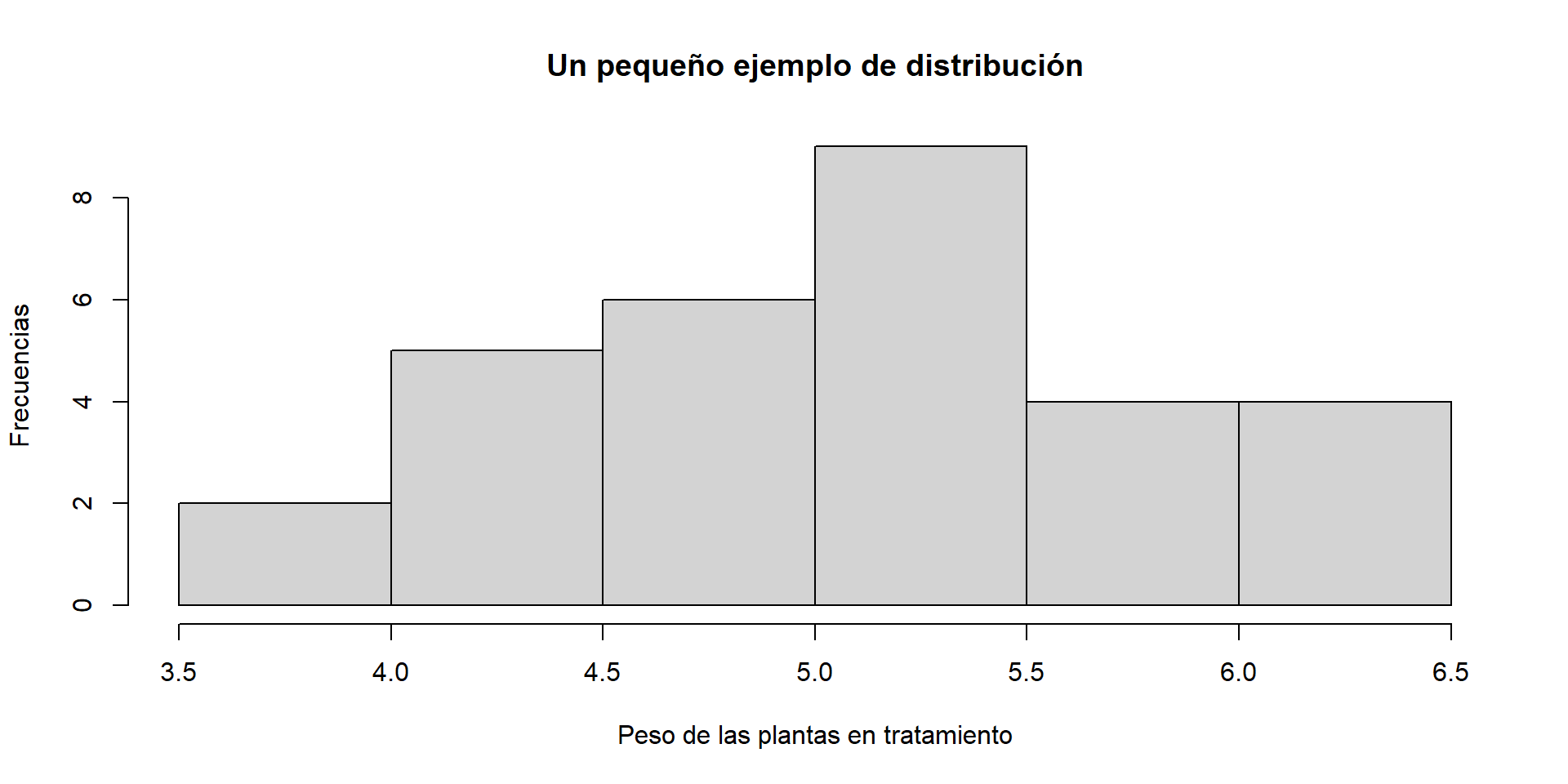
¿Cómo se entienden los datos?

Análisis de datos

Supongamos que partimos con el siguiente ejemplo.

data("PlantGrowth")
attach(PlantGrowth)
planta<-data.frame(PlantGrowth)
planta

   weight group
1    4.17  ctrl
2    5.58  ctrl
3    5.18  ctrl
4    6.11  ctrl
5    4.50  ctrl
6    4.61  ctrl
7    5.17  ctrl
8    4.53  ctrl
9    5.33  ctrl
10   5.14  ctrl
11   4.81  trt1
12   4.17  trt1
13   4.41  trt1
14   3.59  trt1
15   5.87  trt1
16   3.83  trt1
17   6.03  trt1
18   4.89  trt1
19   4.32  trt1
20   4.69  trt1
21   6.31  trt2
22   5.12  trt2
23   5.54  trt2
24   5.50  trt2
25   5.37  trt2
26   5.29  trt2
27   4.92  trt2
28   6.15  trt2
29   5.80  trt2
30   5.26  trt2

¿Qué podemos suponer según nuestros datos?

1. ¿Qué tipos de pruebas podríamos aplicar?
2. ¿Por qué podemos aplicar dichas pruebas?
3. ¿Cuántos grupos tenemos?
4. ¿Qué concluímos en este punto?

Contexto de los datos

Tenemos 30 datos. Se comparan 3 grupos (un control) y dos tratamientos según la variación el peso.
Planteamiento del problema
Variable dependiente: Peso
Variable independiente: Grupo
Formulación de hipótesis

Formulación de hipótesis

Hipótesis	Formulación de la hipótesis	Valor P
Hipótesis nula (HO)	No hay diferencias significativas en el peso de las plantas en los tratamientos	p>0.05
Hipótesis alternativa (H1)	Hay diferencias significativas en el peso de las plantas en al menos uno de los tratamientos	p<0.05

Este será nuestro planteamiento. Lo siguiente que podríamos hacer es hacer una evaluación visual sobre qué tenemos y cómo podemos partir para llegar a una respuesta.

Evaluación de supuestos

Primero hagamos un histograma.

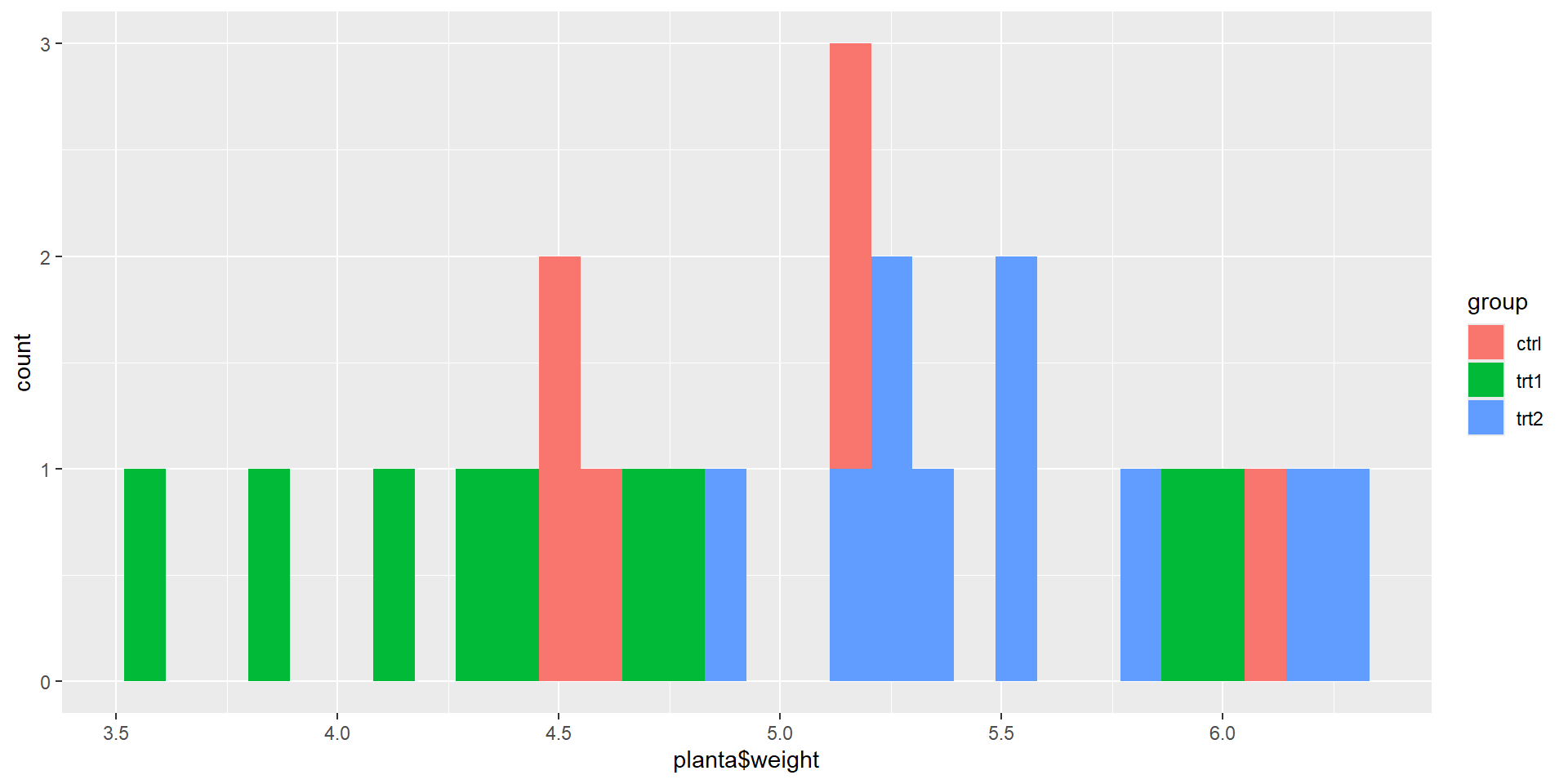
Esta será otra forma más simple de verlo

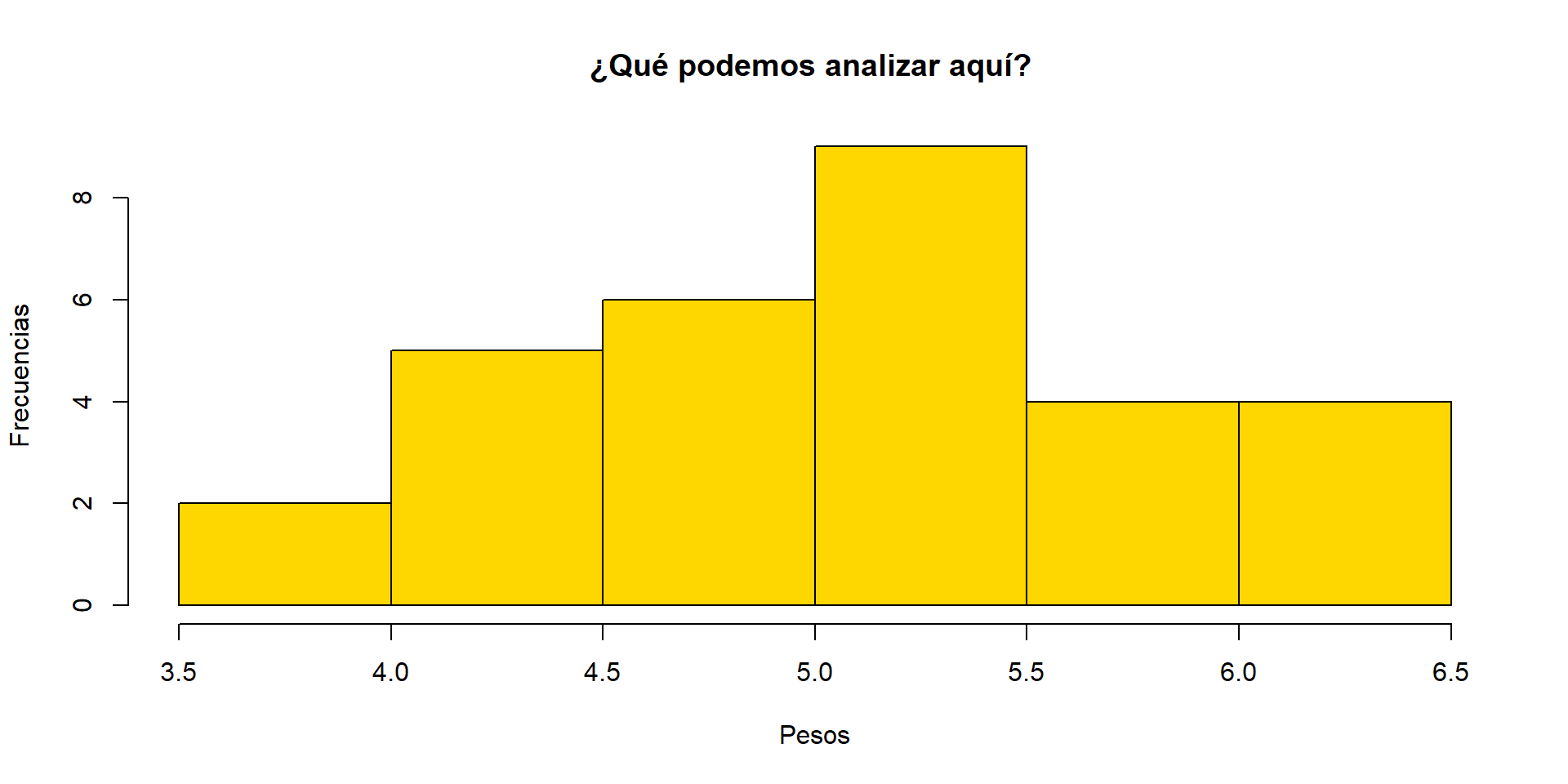
Prueba de Shapiro-Wilk

La prueba de Shapiro-Wilk permite que evaluemos si existe o no normalidad en nuestros datos.

Hipótesis	Formulación de la hipótesis	Valor P
Hipótesis nula (HO)	Nuestros datos se ajustan a la curva de normalidad	p>0.05
Hipótesis alternativa (H1)	Nuestros datos NO se ajustan a la curva de normalidad	p<0.05

Al proceder con la función podemos tener

shapiro.test(planta$weight)

    Shapiro-Wilk normality test

data:  planta$weight
W = 0.98268, p-value = 0.8915

Qué podemos concluir?

Homocedasticidad

La homocedasticidad en este caso se refiere a a la homogeneidad de varianzas. Existen 2 pruebas principales que pueden usarse para seguir con el análisis paramétrico o no paramétrico.
Debemos considerar Levene o Bartlet.

Hipótesis	Formulación de la hipótesis	Valor P
Hipótesis nula (HO)	Nuestros datos se ajustan a la curva de normalidad	p>0.05
Hipótesis alternativa (H1)	Nuestros datos NO se ajustan a la curva de normalidad	p<0.05

Posteriormente aplicamos las pruebas teniendo en cuenta ciertos criterios
Levene es más robusta ante diferencias de normalidad, o existan dudas. Se aplica en cualquier caso. Bartlett es más robusta al detectar variaciones en la normalidad, pero es mejor cuando hay normalidad.

Según lo observado, ¿Qué podemos aplicar?

Ejercicio práctico No. 2

Si hemos observado la normalidad, ¿Qué prueba y bajo que criterio debemos hacerlo?

Aplicación de la prueba

Entendiendo que nuestro valor fue 0.8915 por tanto sugiere p>0.05, entonces, aplicamos Bartlett.

bartlett.test(planta$weight ~ planta$group) #Prueba de Bartlett

    Bartlett test of homogeneity of variances

data:  planta$weight by planta$group
Bartlett's K-squared = 2.8786, df = 2, p-value = 0.2371

library(car)
leveneTest(planta$weight ~ planta$group)

Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  2  1.1192 0.3412
      27               

¿Qué podemos concluir?

Pruebas Paramétricas

Una prueba paramétrica se aplica cuando el criterio de normalidad se cumple tras los supuestos.

Pruebas Paramétricas	Pruebas NO paramétricas
T de Student	Prueba de Wilcoxon - Mann Whitney U test
ANOVA de una vía	Prueba de Kruskal-Wallis
Correlación de Pearson	Correlación de Spearman
Chi cuadrado de independencia	Prueba de Chi-Cuadrado ´Fisher exact test

T de Student

Podemos aplicar la prueba así.

class(PlantGrowth)

[1] "data.frame"

grupo_planta.split <- split(PlantGrowth$weight, PlantGrowth$group)
t.test(grupo_planta.split$ctrl, grupo_planta.split$trt1)

    Welch Two Sample t-test

data:  grupo_planta.split$ctrl and grupo_planta.split$trt1
t = 1.1913, df = 16.524, p-value = 0.2504
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -0.2875162  1.0295162
sample estimates:
mean of x mean of y 
    5.032     4.661 

Nuestro valor p es 0.2504 o sea que p>0.05
¿Qué podemos inferir?

Anova de una vía

La aplicación de ANOVA de una vía implica que tomamos en cuenta una de las colas, o sea hacemos alusión a una de las variables.

anova<-aov(PlantGrowth$weight ~ PlantGrowth$group)
summary(anova)

                  Df Sum Sq Mean Sq F value Pr(>F)  
PlantGrowth$group  2  3.766  1.8832   4.846 0.0159 *
Residuals         27 10.492  0.3886                 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

¿Qué podemos inferir sobre nuestros resultados para la prueba paramétrica?

Pruebas no Paramétricas

Una prueba NO paramétrica se aplica cuando el criterio de normalidad no se cumple tras los supuestos.
Para propósitos del ejercicio aplicaremos usaremos el mismo dataset.

kruskal_wallis<- kruskal.test(PlantGrowth$weight ~ PlantGrowth$group)
kruskal_wallis

    Kruskal-Wallis rank sum test

data:  PlantGrowth$weight by PlantGrowth$group
Kruskal-Wallis chi-squared = 7.9882, df = 2, p-value = 0.01842

¿Qué podemos inferir?

Sobre nuestros resultados obtenidos

En caso de ser una prueba paramétrica. Tendríamos que:

Hipótesis	Formulación de la hipótesis	Valor P
Hipótesis nula (HO)	No hay diferencia significativa entre los grupos	p>0.05
Hipótesis alternativa (H1)	Hay diferencia significativa entre los grupos	p<0.05

En caso de tener una prueba no paramétrica:

Hipótesis	Formulación de la hipótesis	Valor P
Hipótesis nula (HO)	No hay diferencia significativa entre los grupos	p>0.05
Hipótesis alternativa (H1)	Hay diferencia significativa entre los grupos	p<0.05

Entonces, ¿Qué podemos suponer?

Pruebas Pos-hoc paramétricas

Se pueden utilizar cuando se quiere saber la diferencia entre grupos específicos entre sí.
¿Cuándo puede aplicarse?
Pueden aplicarse cuando se cumpla los supuestos paramétricos.
Podemos aplicar la prueba de Tukey que es una prueba paramétrica que combina todas las posibles combinaciones entre grupos para saber cuál es significativamente diferente.

TukeyHSD(anova)

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = PlantGrowth$weight ~ PlantGrowth$group)

$`PlantGrowth$group`
            diff        lwr       upr     p adj
trt1-ctrl -0.371 -1.0622161 0.3202161 0.3908711
trt2-ctrl  0.494 -0.1972161 1.1852161 0.1979960
trt2-trt1  0.865  0.1737839 1.5562161 0.0120064

Pruebas Pos-hoc no paramétricas

Un ejemplo podría ser (Aunque en este caso no es aplicable realmente), sería la prueba de Dunn,que compara pares de grupos con ajustes para múltiples comparaciones. Es la alternativa para Kruskal-Wallis.

library(dunn.test)
dunn.test(PlantGrowth$weight, PlantGrowth$group, method = "bonferroni")

  Kruskal-Wallis rank sum test

data: x and group
Kruskal-Wallis chi-squared = 7.9882, df = 2, p-value = 0.02

                           Comparison of x by group                            
                                 (Bonferroni)                                  
Col Mean-|
Row Mean |       ctrl       trt1
---------+----------------------
    trt1 |   1.117725
         |     0.3955
         |
    trt2 |  -1.689289  -2.807015
         |     0.1367    0.0075*

alpha = 0.05
Reject Ho if p <= alpha/2

¿Qué podemos concluir?

En el caso que sí es adecuado:
Tras la solución de t de student no hay diferencias significativas entre ambos grupos
Tras la solución de ANOVA de una vía concluímos que hay mayor variabilidad entre los grupos y que hay diferencias significativas entre ellos

Muchas gracias